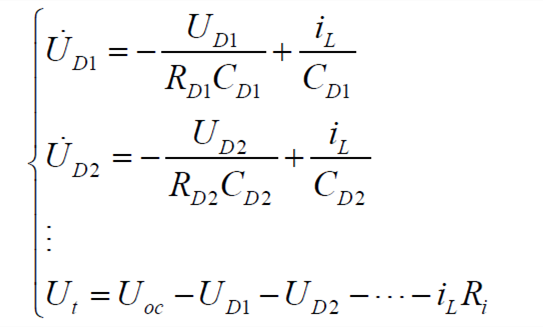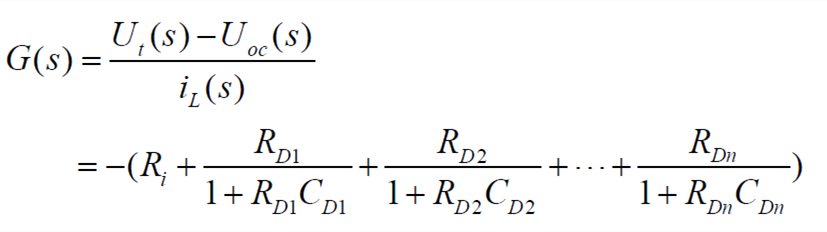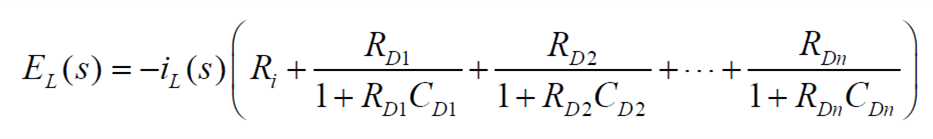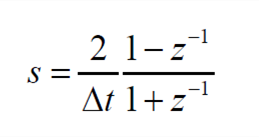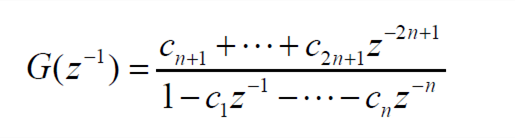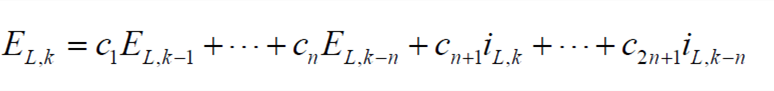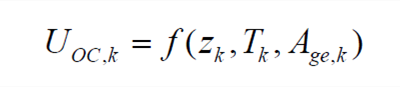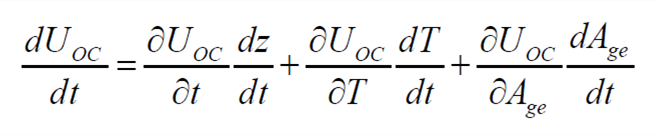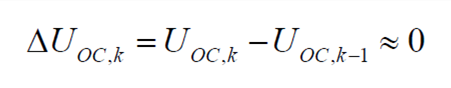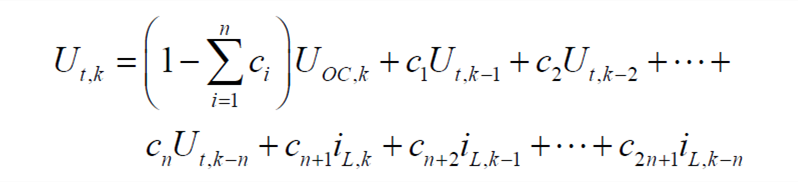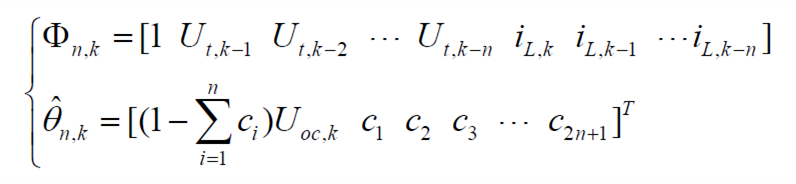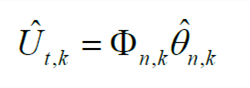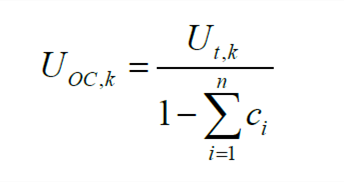等效电路模型
1. 模型介绍
等效电路模型使用传统的电阻、电容、电压源等电路元件组成电路网络来描述动力电池的外特性。该模型使用电压源表示动力电池的热力学平衡电势、使用RC网络描述动力电池的动力学特性。等效电路模型对动力电池的各种工作状态有较好的适用性,而且可以推导出模型的状态方程,便于分析和应用。等效电路模型已广泛应用于新能源汽车建模仿真研究和基于模型的BMS算法开发。下图为典型的由n个RC网络结构组成的动力电池等效电路模型,简称n-RC模型。
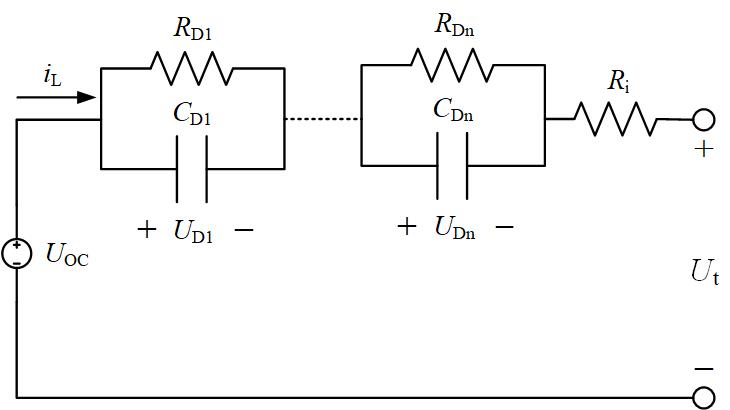
图1 N阶RC等效电路模型结构框图
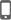
该模型由三部分组成: (1) 电压源:使用开路电压UOC表示动力电池的开路电压; (2) 欧姆内阻:使用Ri表示动力电池电解液、隔膜电阻及各部分零件的接触电阻; (3) RC网络:通过极化内阻RDi和极化电容CDi来描述动力电池的动态特性,其中i=0,……,n。图中,UDi为动力电池的极化电压。根据基尔霍夫电压定律和基尔霍夫电流定律,以及电容电压变化与输入电流的关系,n-RC模型的状态空间方程可表示为:
| (1) |
常用的动力电池等效电路模型有Rint模型、Thevenin模型和双极化(Dual Polarization,DP)模型,分别是n-RC模型在n=0、n=1和n=2时的特例,它们的状态空间方程如表1所示。下面简单介绍这三种常用的等效电路模型。
表1 三种常用的等效电路模型的状态空间方程
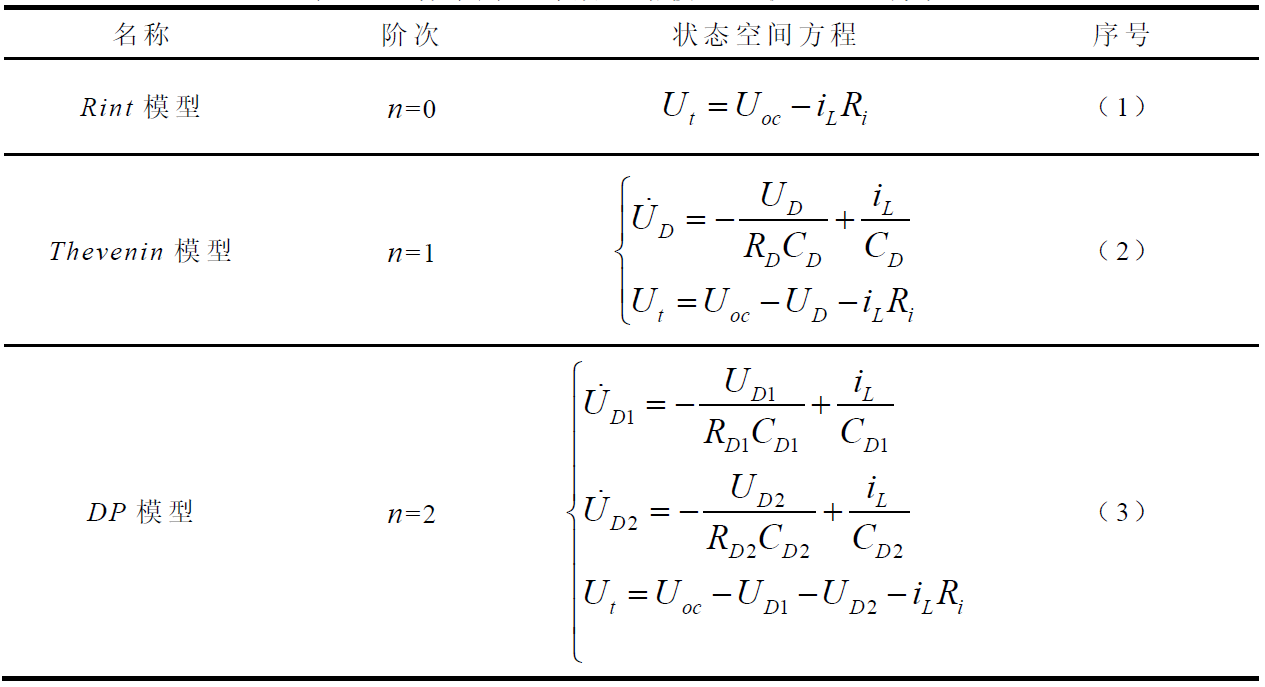
(1)Rint模型使用理想电压源UOC描述动力电池的开路电压,用理想电阻Ri描述动力电池欧姆内阻,UOC和Ri是SOC和温度的函数。Rint模型是最简单的等效电路模型,不含RC网络,它的状态空间方程如表1中式(1)所示。
(2)相比Rint模型,Thevenin模型使用一组RC网络丰富了对动力电池极化特性的描述。该电路模型的状态空间方程如表1式(2)所示,其中,RD和CD分别为极化内阻和极化电容,UD为RC并联环节的电压降,用于模拟动力电池的极化电压。
(3)DP模型在Thevenin模型的基础上又增加了一组RC网络来描述动力电池的极化特性。该电路模型的状态空间方程如表1式(3)所示。
2. 数学方程
为便于BMS应用,需要将模型进行离散化处理,下面以n-RC模型为例推导模型的离散形式。
n-RC模型的传递函数为:
| (2) |
令EL(s)=Ut(s)-UOC(s),则有
| (3) |
采用式(4)所示的双线性变换法将基于s平面的方程(3)映射到z平面。
| (4) |
式中,Δt为系统的采样间隔时间。基于z平面的方程为
| (5) |
式中,ci(i=1,2,…,2n+1)为与模型参数相关的系数。式(5)可以转化到离散时域中,结果为
| (6) |
由于动力电池开路电压与SOC、工作温度T和老化状态Age具有耦合性,定义k时刻的开路电压UOC,k为SOC值zk、温度值Tk和老化状态Age,k的函数,即
| (7) |
则UOC,k对时间的导数可表示为
| (8) |
考虑到BMS的实际采样频率较快,采样时间间隔一般小于1s,因此可做以下三种假设:
假设1:动力电池在单位采样间隔Δt内消耗或吸收的电量对SOC的影响近似为零,即dz/dt≈0。
假设2:动力电池在单位采样间隔内温度不变,即dT/dt≈0。
假设3:动力电池在单位采样间隔内的老化状态不变,即dAge/dt≈0。
基于以上假设,式(8)等于零。则在离散时域中,有
| (9) |
则式(6)可以简化为
| (10) |
定义系统的数据矩阵和参数矩阵为:
| (11) |
则式(10)可以简化为
| (12) |
基于参数矩阵辨识结果,即可实现模型参数的辨识,例如,OCV可以解析为
| (13) |
综上所述,n-RC模型可总结如表2所示。
表2 N阶RC等效电路模型公式

3. 主要结果
图2为等效电路模型电压误差的对比曲线。
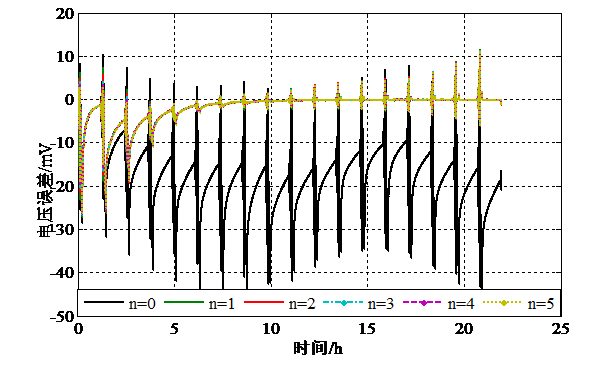
图2 电压估计误差
图2描绘了电压误差随时间的变化关系,表明除Rint模型外,其他等效电路模型结合在线数据驱动的参数辨识方法能够实现可靠辨识,最大误差在30mV以内。
4. 参考文献
[1] 熊瑞. 动力电池管理系统核心算法[M]. 北京:机械工业出版社,2018.(第三章)
[2] H. He*, R. Xiong and H. Guo, “Online estimation of model parameters and state-of-charge of LiFePO4 batteries in electric vehicles”, Applied Energy, vol. 89, no. 1, pp. 413-420, Jan 2012. (下载链接)
[3] H. He*, R. Xiong, H. Guo and S. Li, “Comparison study on the battery models used for the energy management of batteries in electric vehicles”, Energy Conversion and Management, vol. 64, pp. 113-121, Dec 2012. (下载链接)
[4] H. He*, X. Zhang, R. Xiong and Y. Xu, “Online model-based estimation of state-of-charge and open-circuit voltage of lithium-ion batteries in electric vehicles”, Energy, vol. 39, pp. 310-318, Mar 2012. (下载链接)
[5] R. Xiong*, H. He and F. Zhu, “Identification of dynamic model parameters for ultracapacitor used in electric vehicles”, Journal of Beijing institute of technology, vol. 20, no. suppl.2, pp.204-210, Dec 2011. (下载链接)
[6] C. Lin, H. Mu and R. Xiong*, “Multi-model probabilities-based state fusion estimation method of Lithium-ion battery for electric vehicles: state-of-energy”, Applied Energy, 2017, vol. 194, pp. 560-568, May 2017. (下载链接)
5. 可用资源
(1) 等效电路模型资料: 点击下载(![]() PDF水印教材)
PDF水印教材)